For symmetric integration of even or odd functions, you can show that the following relationship is true:

\[\int^a_{-a} f(x) dx = \begin{cases} 0 & \text{if $f(x)$ is an odd function}\\ 2\int^a_0 f(x)dx & \text{if $f(x)$ is even} \end{cases} \tag{1}\]

Even functions are classified as those where the following relationship holds: $f(-x) = -f(x)$. Odd functions, on the other hand, as classified as follows: $f(-x) = f(x)$.

Looking at the graphical representation of the even and odd functions, it becomes obvious why the above relation is true: the negative integral of the odd function will cancel itself out with the positive portion, while the even function is symmetric about the y-axis:

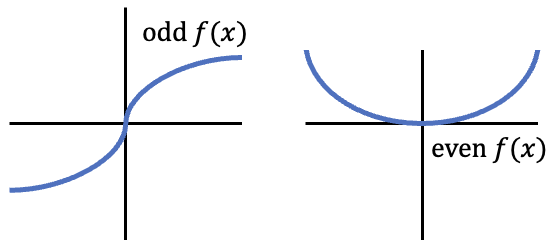
The derivation of the above definitions starts with the decompositions of the integral function.

\[\int^a_{-a} f(x) dx = \int^0_{-a} f(x) dx + \int^a_0 f(x) dx \tag{2}\]

Looking at the first term on the RHS, we can substitute $u = -x$ and $-du = dx$:

\[\int^{x=0}_{x=-a} f(x) dx = \int^{u=0}_{u=a} f(-u) (-du) = -\int^0_{a} f(-u) du = \int^a_{0} f(-u) du\]

With this final form, we can simply rename the $u$ variable back to $x$:

\[= \int^a_{0} f(-u) du = \int^a_{0} f(-x) dx\]

Substituting back into equation $(2)$ then becomes

\[\int^a_{-a} f(x) dx = \int^a_0 f(-x) dx + \int^a_0 f(x) dx\] \[\int^a_{-a} f(x) dx = \int^a_0 \left[ f(-x) + f(x)\right] dx \tag{3}\]

Now for an odd function where

\[f(-x) = -f(x) \quad \text{or} \quad f(x) + f(-x) = 0\]

the integral is zero. For an even function

\[f(-x) = f(x) \quad \text{or} \quad f(x) + f(-x) = 2f(x)\]

which then implies

\[\int^a_0 \left[ f(-x) + f(x)\right] dx = 2 \int^a_0 f(x) dx\]

References

Greenspan, Harvey Philip, and David J. Benney. “Calculus: an introduction to applied mathematics.” (1973). pp. 239-240