Link to integration
Brownian Diffusion
Einstein’s solution to the problem of Brownian motion can be considered to be the beginning of stochastic modeling of natural phenomena. His solution the Brownian diffusion problem has two major findings with regards to the motion of a pollen grain:
- Motion is caused by high frequency impact on the pollen grain by the liquid molecules that the grain is suspended in.
- The motion and frequency of these impacts is so high and complicated that their effects on the pollen grain can only be described probabilistically in term of “exceedingly frequent statistically independent impacts”.
The building blocks of the derivation rest on the following assumptions:
- Each particle has its own motion that is independent from the motion of other particles.
- The movements of a single particle through time is also considered to be independent processes, as long as the time period chosen between movements is not too small.
- A time interval $\tau$ is chosen such that it is small compared to observable time periods but large enough such that the motions of a given particle can be considered to be independent of one another.
- A total of $n$ particles are suspended in a liquid and during the time $\tau$, the individual particles will travel a distance $\Delta$. For each particle, $\Delta$ will have either a positive or negative value. A number of particles, expressed as $dn$, which will move between $\Delta$ and $\Delta+d\Delta$ is expressed by the following equation:
The probability density function, $\phi\left(\Delta\right)$, obeys the following: \(\int^{\infty}_{-\infty}\phi\left(\Delta\right)d\Delta = 1 \tag{2}\) and \(\phi(\Delta) = \phi\left(-\Delta\right) \tag{3}\)
We restrict ourselves to the reference case where the number of particles per unit volume, $v$, depends only on $x$ and $t$. As such, $v = f\left(x, t\right)$ is the equation expressing the number of particles per unit volume. The distribution of particles is calculated between time intervals $t$ and $t+\tau$.
The objective is to first find the number of particles at time $t+\tau$ which are between two planes perpendicular to the x-axis and passing through the points $x$ and $x+dx$.
Starting out with a simple figure, the number of particles at a certain point of $x$ and $t$ are defined by $f\left(x, t\right)$. As such, the number of particles between some infinitesimally small distance $dx$ is depicted in the figure below:
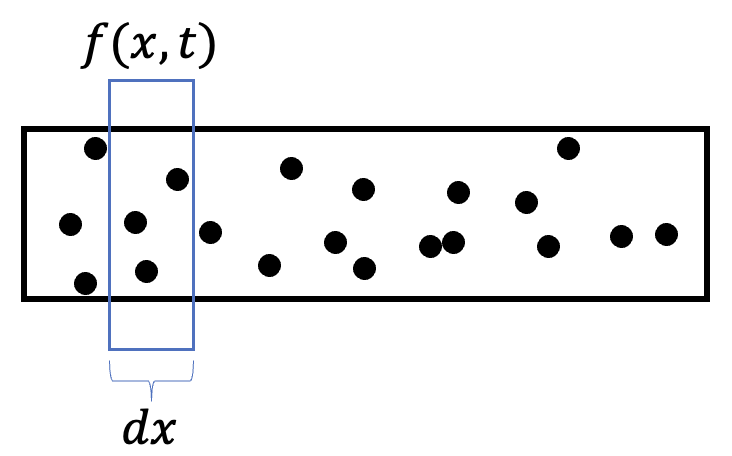
The adding a second cross-section that is $\Delta$ distance away yields the following:
By definition, the probability that a certain number of particles will move by a distance of $\Delta$ is $\phi\left(\Delta\right)$. As such, the probability some molecules will move to the area defined by $f\left(x, t+\tau\right)$ can be defined by the integral of the probability density function over the full range of $\Delta$ values multiplied by the function of particles per unit area at the distance $\Delta$ away from the end location:
\[f\left(x, t+\tau\right)dx = \int^{\infty}_{-\infty} f\left(x+\Delta, t\right)dx \phi(\Delta) d\Delta\]rearranging yields
\[f\left(x, t+\tau\right)dx = dx \int^{\infty}_{-\infty} f\left(x+\Delta, t\right) \phi(\Delta) d\Delta\]The $dx$ terms can be crossed out
\[f\left(x, t+\tau\right) = \int^{\infty}_{-\infty} f\left(x+\Delta, t\right) \phi(\Delta) d\Delta\]The left-hand-side of the above equation can written as
\(f\left(x, t+\tau\right) = f\left(x,t\right) + \tau \frac{\partial f}{\partial t}\) The right-hand-side function within the integral can be expanded using a Taylor series
\[f\left(x+\Delta, t\right) = f(x,t) + \Delta \frac{\partial f(x,t)}{\partial x} + \frac{\Delta^2}{2!}\frac{\partial^2 f(x,t)}{\partial x^2} + ...\]Plugging the above two equations back into the original integral yields
\[f + \tau \frac{\partial f}{\partial t} = f \int^{\infty}_{-\infty} \phi(\Delta) d\Delta + \frac{\partial f}{\partial x} \int^{\infty}_{-\infty} \Delta \phi(\Delta) d\Delta + \frac{\partial^2 f}{\partial x^2} \int^{\infty}_{-\infty} \frac{\Delta^2}{2} \phi(\Delta) d\Delta\]where $f = f(x, t)$.